纯JS实现比特币压缩公钥转成非压缩公钥

作者:王建伯 时间:2021年12月29日 微博:比特币布道者 一、背景 1、椭圆曲线 (1)有限域(Fp)椭圆曲线 有限域椭圆曲线Ep(a,b),p为质数,x,y∈[0,p-1] y^2 = x^3 + ax + b (mod\ p)y2=x3+ax+b(mod p) 其中,a、b是小于p的非负整数,且满足: 4a^3 + 27b^2 ≠ 0 (mod\ p)4a3+27b2=0(mod p) (2)椭圆曲线加密(ECC)参数要求 通常将有限域上的一条椭圆曲线描述为T = (p,a,b,G,n,h)。 其中,p、a、b确定一条椭圆曲线,p为质数,(mod p)运算,G为基点,n为点G的阶(即nG = 0),h为协因子,是椭圆曲线上所有点的个数m与n相除的商的整数部分。 参量选择要求:
(3)比特币所选椭圆曲线 比特币系统选用的secp256k1中,参数为 p = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F,即2^{256} − 2^{32} − 2^9 − 2^8 − 2^7 − 2^6 − 2^4 − 12256−232−29−28−27−26−24−1 a = 0, b = 7 G=(0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8) n = 0xFFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 h = 01 (3)公钥坐标 公钥 = 私钥k * 基点G,公钥是椭圆曲线上的点,可以用坐标(x,y)表示。 椭圆曲线y^2 = x^3 + 7y2=x3+7在实数域的图形如下:
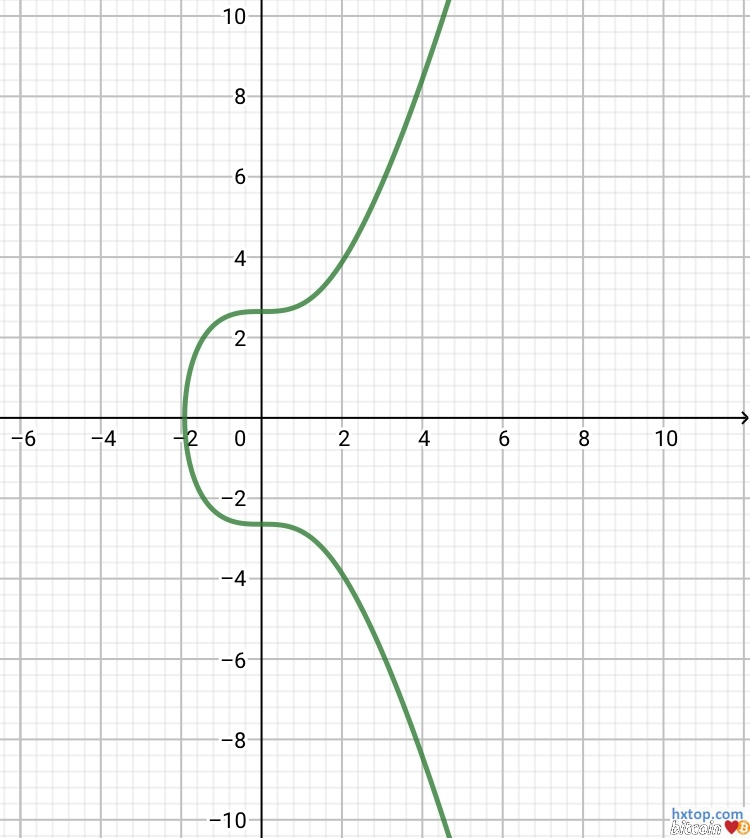
可知,曲线以x轴为对称轴上下对称,且曲线上的点的坐标(x,y)中的y值可以通过方程式由x计算出来。 所以,公钥坐标可以采用“x值”加“y值的正负标志位” 来表示。 由于,在有限域上y值只能为正值,因为-y mod p = p – y,坐标(x,-y)%p等价于(x,y)%p,可以参考下图:
所以,无法通过y值直接判断y值的正与“负(来自-y mod p) ” ,理论上存在的判断方法至少有两种: 1)将公钥坐标(x,y) 带入实数域曲线方程y^2 = x^3 + 7y2=x3+7。如果等式成立,说明y值为正,否则y为“负”,来自-y mod p。 2)利用公钥坐标(x,y)中y值的奇偶性来判断y值正负,原理如下: 由于p是质数,所以当y是偶数时,p – y (即-y mod p)是奇数,当y是奇数时,p – y (即-y mod p)是偶数,且由于通过x值和方程式计算出的y值只会在正数域。 所以,当公钥y值在“负”数域时 ,那么其在正数域的对称点p – y(即为通过x值和方程式计算出的y值)的奇偶性必然与其相反。 那么,就可以通过y的计算值与真实值的奇偶性的对比,来判断y值的正负。当二者一致时,y值为正;当二者不一致时,y值为负,来自-y mod p。 2、节省区块空间 在实施SegWit之前,每笔交易的见证数据(Sigscript)包括签名及公钥是占区块空间的,通过实施压缩公钥,可以有效降低见证数据大小,从而节省区块空间。 (1)非压缩公钥:04+x坐标+y坐标。 (2)压缩公钥:y坐标的奇偶标志位+x坐标。当y为偶数时,奇偶标志位记为偶数标志02;当y为奇数时,奇偶标志位即为奇数标志03。 二、JS代码实现 1、二次剩余 计算y^2 = x^3 + 7 (mod\ p)y2=x3+7(mod p)中的y值: (1)首先,计算(x^3 + 7) mod\ p(x3+7)mod p,根据模计算公式,可知: (x^3 + 7) mod\ p(x3+7)mod p (2)最后,计算y^2 = n (mod\ p)y2=n(mod p),这其实就是在求解二次剩余问题。 根据定理:如果p是质数,p mod 4 = 3,且n是模p的二次剩余,那么±n^{\frac {p+1}{4}}±n4p+1是y模p的平方根。 又根据secp256k1参数p,可知p mod 4 = 3,所以可以用上述定理求解y值。 1)根据费马小定理:如果p是质数,而整数y不是p的倍数,那么y^{p-1} ≡ 1(mod\ p) yp−1≡1(mod p) ,来证明上面的定理。 ∵y^2 = y^2 × 1 = y^2 × y^{p-1} = y^{p+1}(mod\ p)∵y2=y2×1=y2×yp−1=yp+1(mod p) ∵p\ mod\ 4 = 3∵p mod 4=3 ∴y = ±y^{2 × {\frac {p+1}{4}}}(mod\ p)∴y=±y2×4p+1(mod p) 2)根据欧拉判别条件:如果p是奇质数(大于2的质数),整数n不是p的倍数,n是模p的二次剩余的充要条件是n^{\frac {p-1}{2}} ≡ 1(mod\ p)n2p−1 ≡1(mod p),来证明上述定理。 ∵y^2 = y^2×1 = n×n^{\frac {p-1}{2}} = n^{\frac {p+1}{2}}(mod\ p)∵y2=y2×1=n×n2p−1=n2p+1(mod p) ∵p\ mod\ 4 = 3∵p mod 4=3 ∴y=±(n^{\frac {p+1}{2}})^{\frac{1}{2}} = ±n^{\frac {p+1}{4}}(mod\ p)∴y=±(n2p+1)21=±n4p+1(mod p) 2、JS代码 注:压缩公钥及非压缩公钥验证生成工具http://BTC.mom/bitcoin 需要引入bitcoinjs-min.js文件 见压缩包:CompressToUnompressPubkey var compressedPubkey = "0399c976ed4adf6a58acd8dc7c916f8aa23df82c181125ac3d9d1e8cf2b110a2b3"; var p = "fffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f"; //根据模公式,可知y^2 = (x^3 + 7) mod p = (x^3 mod p + 7) mod p
var uncompressedPubkey = "04" + compressedPubkey.slice(2,66) + Crypto.util.bytesToHex(integerToBytes(y)); |



 网友评论
网友评论


 @好耶网络
Processed In:-0.3477-Seconds, CMS-8Queries-Amazon Web Services
@好耶网络
Processed In:-0.3477-Seconds, CMS-8Queries-Amazon Web Services
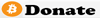











 您的位置:
您的位置: 【】
【】
 [上两篇]
[上两篇]